Data and statistics are often used in research but these two terms have different distinctions. Data refers to the pieces of information recorded and gathered for the purpose of analysis. Descriptive statistics, on the other hand, is the result of the analysis made through the data gathered.
In order for you to be able to gather data in your statistical study, you have to first determine the population – which can be a group of people, or things, depending on the subject of your descriptive research. A collection of data of one or more variables is called a data set. A variable has two main types: categorical and numerical. Categorical represents data that is qualitative while numerical represents quantitative data. A categorical variable can either be nominal or ordinal. On the other hand, numerical variables are either discrete or continuous.
Contents
Role of Statistics in Research
The role of statistics in research is to be used as a tool in analyzing and summarizing a large volume of raw data and coming up with conclusions on tests being made. The study of statistics is classified into two main branches: descriptive statistics and inferential statistics. Inferential statistics are used for hypotheses testing and estimating the parameters of a population while descriptive statistics is the way of summarizing and organizing sets of data to make it more easily understood by the audience it is meant for. It often describes information through patterns and graphs.
The first and foremost steps being used in data analysis, as it is difficult to analyze raw data in large volumes. Before you are able to go further on your research, you have to first gather and simplify your data sets.
There are two methods in descriptive statistics: the numerical method and the graphical method.
Descriptive Statistics and Numerical Methods
Descriptive statistics involves averages, frequencies, and percentages for categorical data, and standard deviations for continuous data. The statistical measures used in descriptive statistics are the measures of central tendency, measures of spread, and measures of skewness.
A measure of central tendency represents the central point of a dataset which involves the mean, median, and mode. Mean, also called as the average, is simply the sum of the data sets divided by the number of terms. The median, on the other hand, is the value in the middle of a data set while the mode is the number that appears the most in a data set.
If the total number of terms in a data set is an even number, you have to get the two values in the middle and solve for its average to be able to get the median. It is also possible to find more than one mode in a data set which is called multimodal.
A measure of spread, also called as the measure of dispersion, describes the variability of the values in a data set. It involves the computation of range, variance, standard deviation, and quartiles.
The range tells the value of the distance between the lowest and the hight value. Standard deviation is the measure of dispersion in the center of the value, while the variance is the expectation square of the standard deviation.
A quartile is classified into three parts: The first quartile or the Q1 is the middle number between the lowest value and the median of the data set. The second quartile (Q2), is the median of the data, while the third quartile (Q3) is the middle value between the median and the highest number in the data set.
Skewness is the degree of distribution of a variable about its mean. The value of skewness can either be positive, negative, or undefined. When the result is zero, it means that no skewness has occurred.
Descriptive Statistics and Graphical Methods
In descriptive statistics, graphs are used to visualize data analysis and plot data sets. The most common graphs used are pie graphs, bar graphs, line charts, and histograms. Other types of graphs that are less common are the dot plots, and dots and whiskers charts.
Pie Chart
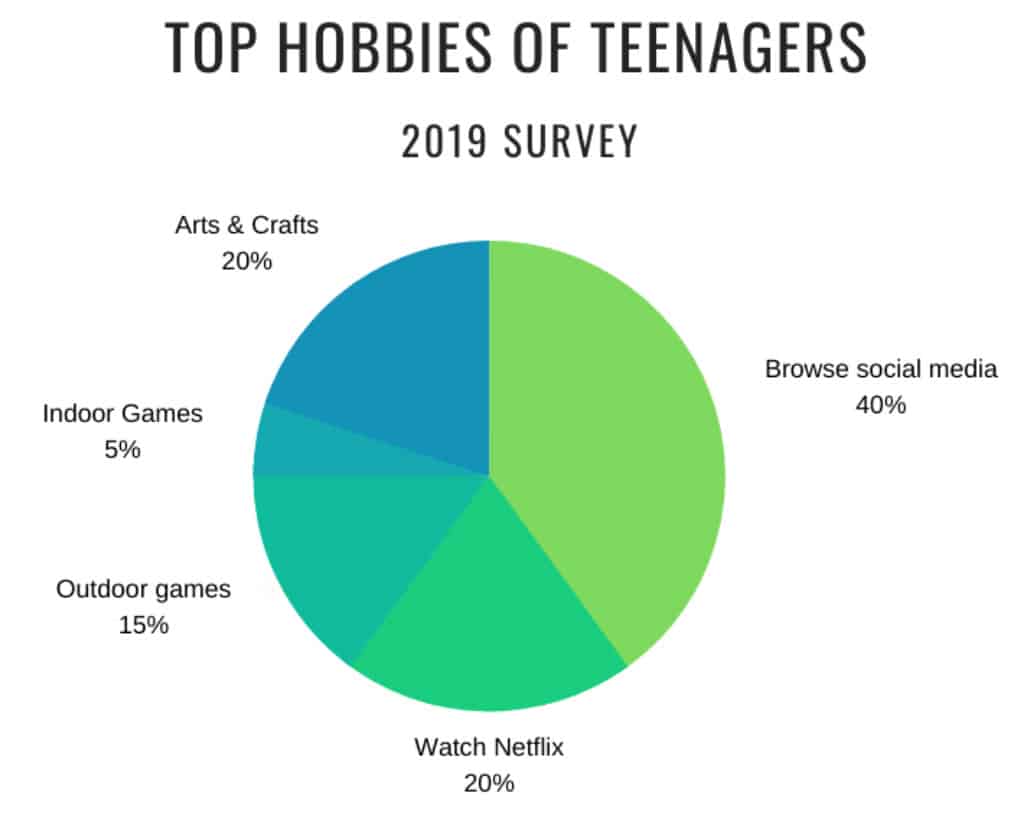
The pie chart is a circular chart to describe a numerical proportion. It is often divided into slices proportionally based on the quantity it represents. In the example below, assume that you created a survey for teenagers to know their top hobbies. On a scale of 100 teens, 40 of them often browse social media which makes it the highest among other hobbies mentioned. Indoor games being 5% based on the pie chart is the least favorite hobby of teenagers.
Line Charts
A line chart or line graph is a type of chart that illustrates data sets without a specific numerical proportion. It is best and most often used to represent sequential orders and trends over time. For example, you have recently set up a business selling sweet treats. Each week you have used different types of marketing approaches. For you to be able to determine what kind of marketing strategy worked best, you have to illustrate and analyze the sales you’ve made each week.
Bar Graph
Bar graphs illustrate categorical data with vertical or horizontal rectangular bars as their values. Through a bar graph, the viewer can compare data easily at a glance. Pie charts represent proportion as a whole while bar graphs illustrate each bar with different values or categories. For example, you are selling different ice cream flavors. To know which are the best sellers, you can simply draw a graph presenting each flavor and the number of ice cream being sold. We can easily determine in this graph that the dark chocolate flavor has the most number of ice cream being sold and vanilla being the least among other flavors.
Analyzing data can be both easy and complicated. With descriptive statistics, we can easily describe and simplify a large volume of raw data and convert it into something that can be easily understood by our viewers. From illustrating the number of sales in the business up to the analysis needed for machine learning, descriptive statistics help us go further beyond every research and know the other steps necessary for data analysis.
Image by rawpixel